Olympiades internationales de mathématiques – Kézaco et à quoi ça sert ?

Tout le monde connaît les jeux olympiques (autrement appelés Olympiades) où tous les 4 ans s’affrontent les meilleurs athlètes de chaque nation, la sélection de ces athlètes se faisant suivant un protocole assez compliqué.
Afin de contenir l'expansion, le nombre d'athlètes participants aux Jeux est désormais plafonné à 10 500 en été et les participants doivent désormais réaliser des minima dans les disciplines chiffrées ou profiter de quotas olympiques gagnés lors des grandes compétitions précédant les jeux. Pour permettre à toutes les nations de participer, les minima sont à géométrie variable selon les nations et un Comité olympique n'ayant aucun athlète qualifié aux Jeux profite d'invitations, généralement en athlétisme, natation, judo ou haltérophilie pour les Jeux d'été.
Nul n’est besoin de rappeler l’enjeu global de ces jeux, aussi je ne le ferais pas.
Par contre il est très intéressant d’établir des corrélations entre certains paramètres pour aboutir à certaines conclusions.
Par exemple il semble évident que plus un pays a de licencié dans un sport –disons l’escrime- plus il a de chance de remporter une médaille.
La corrélation entre le nombre total d’habitant et le nombre de médaille gagnée en escrime est beaucoup moins évidente. En effet il faut affecter à ce nombre d’habitant un coefficient culturel directement lié à l’intérêt que ces mêmes habitants portent à l’escrime (pour revenir à cet exemple). En France ce coefficient aurait un effet multiplicateur au vu du poids historique de cette discipline, donc du nombre de licencié et par voix de conséquence de son financement.
Nombre de licencié en 2015 : 53635
Je ne pense pas que ce coefficient soit le même en France qu’au Japon -pays où historiquement le sabre, le fleuret ou l’épée n’existaient pas.
Le mal que j’ai eu à trouver sur Internet le nombre de licencié pratiquant l’escrime au Japon a été récompensé par la validation de la justesse de mon hypothèse de départ : ce nombre est très faible. Il est de 6000.
De ces chiffres on tire le tableau suivant :
| France | Japon | |
| Population (en millions) | 66,9 M | 127 M |
| Licenciés | 53635 | 6000 |
| Nombre de médaille JO 2016 | 143 | 2 |
En première lecture il ressort clairement que sur le plan pur des médailles la France écrase le Japon dans un rapport de 71,5 à 1. Cependant si l’on ramène le nombre de médaille au nombre de licencié, cet avantage n’est alors plus aussi net. On compare 0,0026 à 0,0003 dans un rapport de 8,6 à 1.
Autrement exprimé : si les 6000 japonais avaient été 53635 avec un taux de succès de 2/6000 ils auraient obtenu 17,8 médailles.
Ou encore ; un escrimeur français a 8,6 fois plus de chance d’obtenir une médaille que son homologue japonais.
A quoi faut-il attribuer cet avantage ?
A une anomalie statistique : Les principaux espoirs japonais auraient été absents du tournoi ?
A une anomalie culturelle : Les sports d’épée (au sens large) n’attireraient que l’élite de la société japonaise qui, misant sur la qualité plutôt que sur la quantité, se priveraient de l’effet exponentiel des grands nombres ?
A la validité d’un cliché grassement xénophobe : Les japonais ne font que copier les occidentaux sans les égaler !?
La réponse à ces questions est à chercher en examinant les chiffres d'un autre type d'Olympiades -les Olympiades Internationales de Mathématiques ou OIM- et qui procède exactement du même cheminement avec la particularité rare de rassembler toutes les données ou preuves dans un seul site : le site de l'OIM.
Ce faisant nous allons aussi découvrir beaucoup plus qu'une simple problématique de stratégie de développement d'un art.
Mais avant de se concentrer sur les chiffres de l'OIM un retour historique est nécessaire.
Napoléon le proclamait : « nul ne peut bachoter en mathématiques ». Il entendait par là que tout un chacun peut ingurgiter un savoir parfois encyclopédique, mais que la seule matière qui n’en permettait pas la restitution « livresque » étaient les mathématiques.
Ce court aphorisme est beaucoup plus clairement expliqué par Leon Henkin (mathématicien américain) par le biais du livre « La chasse aux trésors mathématiques » :
« L'une des plus grandes méprises à propos des mathématiques, que nous perpétuons dans nos salles de classe, c'est que le professeur semble connaître les réponses de tous les problèmes qui sont traités. Cela donne l'impression à l'élève qu'il y a quelque part un livre contenant toutes les réponses intéressantes, et que les professeurs connaissent ces réponses. Et que, si nous pouvions mettre la main sur ce livre, ce serait réglé. C'est tellement contraire à la vraie nature des mathématiques. »
Cette vision napoléonienne a tellement marqué la France que depuis, le règne des mathématiques, mal enseignées, a durablement martyrisé nombre de petits français.
C’est la matière reine discriminante. Et ce dans tous les domaines. Dès que l’on veut introduire un peu de sélectivité, il suffit d’introduire une épreuve de math !
Quel concours, un peu généraliste, n’a pas son épreuve de math ? Quasiment, pour être sûr de ne pas en avoir, il faut passer l’agrégation de philosophie ! Et encore...
Pour vous en convaincre (et je cite de mémoire) : en 1985 le concours de commissaire de police comportait des épreuves portant tout naturellement sur le Droit : constitutionnel, pénal, procédure pénale et … en option une épreuve de math (sic) !
Apparté. Hé non...Je n'ai pas été reçu...
Napoléon a donc misé sur les maths pour sélectionner ses élites via l’école spéciale militaire de St Cyr (qu’il a créée en 1802) et via l’école polytechnique (qu’il a remanié en 1804). Cependant ce qu’il avait redouté – le rétablissement des rentes de l'éducation- est arrivé.
La classe supérieure a contourné cette sélectivité mathématiques en réintroduisant le bachotage MAIS au profit de sa progéniture, tout en en privant soigneusement celle de ses concurrents moins-disant socialement, la laissant s'y heurter de plein fouet.
Un bon exemple en est donné à l’époque d’Evariste Galois. Cette étoile filante des mathématiques a été recalé 2 fois au concours d’entrée de Polytechnique en 1828 et 1829 car il insupportait par son arrogance ses examinateurs. Pour des raisons alimentaires il a dû se rabattre sur le concours de l'Ecole Normale. Pendant ce temps, ses contemporains du Lycée Louis-le-Grand entraient en math sup parallèlement à leur entrée en classe de réthorique (soit notre première actuelle) – ce qui à l’époque était possible. Cela leur permettait de passer le concours d'entrée de l'X dés l’âge de 18 ans au sortir de la classe de math spé.
Conséquence : entre leur première tentative à 18 ans et la limite d’âge de 23 ans, ils disposaient de 4 à 5 tentatives. Et revoilà le bachotage qui repointe son museau.
Napoléon avait-il raison ? Les maths même « bachotées » sont-elles encore suffisamment sélectives ? Et en quoi ?
Une épreuve hautement élitiste subsiste encore en France. Il s’agit du Concours général. Cette épreuve -créée en 1747 et dont la tradition a perduré au fil des siècles- a ceci d’anti-bachotage que les élèves de Première ou de Terminale, qui en passent l’épreuve ne le font qu’une seule fois. Puisqu'on ne redouble plus, qui va réclamer et surtout obtenir le redoublement dans le but express de repasser cette épreuve en cas d’échec ?!
Pour ce qui est des maths, il n’est pas rare que ceux qui en obtiennent le premier Prix reçoivent de très honorables distinctions par la suite. A l’instar de Jean-Christophe Yoccoz, 1er prix du Concours général, médaille d’argent en 1973 puis d’or en 1974 aux olympiades internationales de mathématiques, puis 1er au concours d’entrée à l’ENS, 1er à l’agrégation de mathématiques, et pour finir médaillé Fields en 1994.
Ou encore de Laurent Lafforgue qui obtient un Premier accessit au Concours général de version latine en Première puis le premier prix au Concours général de mathématiques en Terminale. Fort de ces deux prix il obtient (entre autres) en 2002, la médaille Louis Fields.
A quoi sert ce type d'épreuve ? Il existe autant de réponses qu'il existe de sensibilités humaines.
Plutôt qu'essayer d'y répondre il faut plutôt se poser ces questions suivantes : Quand une société est-elle capable d'organiser une telle épreuve ? Quand en éprouve-t elle le besoin ? Pourquoi en a-t elle besoin ? Et pour finir la question fondamentale de synthèse et qui est la plus polémique :
Qui a besoin de matheux et pourquoi en a-t-on besoin ?
Notre société occidentale capitaliste et matérialiste en a un besoin impérieux. Car toutes les autres matières scientifiques s'appuient sur les maths. Et même mieux : des avancées en maths ne seront exploitées que bien plus tard par les autres domaines car soit la technologie ne suivait pas, soit le concept physique qui se cachait derrière était trop novateur pour l'époque.
Le livre de Ian Stewart « 17 équations qui ont changé le monde » le rappelle à chacun des ses chapitres. Il organise son livre en chapitre qui pédagogiquement commencent toujours par une unique page d'introduction subdivisée en 4 parties : « Exposé de l'équation », « Ce que cela nous dit » , « Pourquoi c'est important » et « A quoi cela nous a conduit ».
Je vais juste présenter de façon très, très raccourci l'un de ses exemples :
En 1614 Napier et Briggs – deux mathématiciens anglais- inventent les logarithmes.
En 1632 un autre mathématicien anglais -William Oughtred- en tire la très concrète règle à calcul qui était -je le rappelle pour les lecteurs qui ont eu 18 ans après 1975- l'équivalent de nos calculettes scientifiques actuelles.
Ces avancées en math pures produisent de la technologie. Ce qui convient parfaitement à notre mode de vie occidental.
Mais si un pays, une société ne veut pas suivre notre modèle et se satisfait d'une vie simple, sans technologie, sans matheux dont on ne transposerait les travaux sur le plan matériel, peut-il vivre selon ce concept ? La sanction tombe comme un couperet : ce pays se fera gober tout cru par celui porté par la technologie. Aldous Huxley le décrit magistralement dans son livre « Iles ».
Apparté : oui je sais...Ce n'est pas déontologique de renvoyer les lecteurs à un autre lien avant de poursuivre le fil de cet article mais je ne peux faire autrement car même le résumé via le lien ci-dessus est trés long, mais en plus ne rend pas compte de toute la complexité de la situtation. Aussi je vous enjoins instamment d'au-moins lire ce résumé.
Est-il concevable qu'un pays investisse énormément dans l'éducation aux mathématiques sans en exploiter les fruits directement via la technologie qui fatalement en découle ? A ma connaissance, à l'heure actuelle la réponse est non.
Il ne reste donc que deux alternatives : enseigner les maths et participer à la compétition internationale technologique ou ne pas l'enseigner et donc ne pas y participer.
Ceux qui ont choisi la 2ième possibilité ont deux sous-choix : acheter la technologie provenant d'autres pays (grâce aux ressources de son sous-sol ou de ses banques, si ces ressources existent) ou alors subir/consentir la domination d'autres pays.
Pour ceux qui ont suivi la première voie se pose le choix du moyen de l'enseignement des maths. L'exemple initial de l'escrime est parfaitement représentatif : on chouchoute une élite dont il sort quelques pépites ou on investit massivement dans le nombre dont il en sortira beaucoup. Entre ces deux tactiques, à chaque extrémité du spectre de possibilité, il existe tout une palette de choix qui panache l'un et l'autre.
Mais il faut bien garder à l'esprit qu'éduquer sa jeunesse a un coût lequel ne produit pas toujours le résultat espéré. Ainsi décider de mener tous ses jeunes jusqu'au niveau 3ième et s'arrêter là coûte moyennement cher mais ne produira que de la technologie du 19ième siècle (à vue de nez et pour prendre un exemple caricatural).
Tout ceci est bien théorique. Retrouve-t-on cela dans des chiffres ?
Reprenons cette épreuve typiquement française (le Concours général) qui s’adresse à un public du secondaire ; elle a son pendant au niveau planétaire dans le domaine des sciences : ce sont les Olympiades Internationales de Sciences auxquelles appartiennent l'OIM.
Attachons-nous aux Olympiades Internationales de Mathématiques ou OIM.
Les Olympiades internationales de Mathématiques, comme son nom ne l’indique pas, ont lieu chaque année dans un pays différent. Les participants (au nombre de 6 par pays depuis 1983) sont issus du secondaire.
Son site officiel nous donne des statistiques en tous genres. Commençons par celle-ci :
https://www.imo-official.org/results.aspx
Un premier constat frappe le regard : le tableau est presque vide en partie droite vers les années 1959 (création de l’épreuve) ; puis au fil des ans des chiffres viennent l’étoffer.
Si on ne regarde que les pays inscrits en 1959 on voit bien que c’était un truc de feu le Pacte de Varsovie : URSS, Pologne , Bulgarie, Roumanie, Tchécoslovaquie, Hongrie et RDA.
Une sorte de compétition amicale s’instaure entre pays d’obédience communistes.
Puis petit à petit la Yougoslavie (1963), la Mongolie (1964), la Finlande (1965) viennent compétiter. Là encore on comprend que les satellites de l’URSS adhèrent à ce projet.
Puis d’un coup arrivent la France, la Suède, le Royaume-Unis et l’Italie (1967).
Que s’est-il passé ? Nous sommes à la veille de l’union douanière de la CEE qui aura lieu en Juillet 1968. La Suède et le Royaume-Unis n'étant pas concernés, il s’agit d’autre chose. Voilà une première interrogation intéressante à laquelle je n'ai pas de réponse.
Puis petit à petit de plus en plus de pays vont adhérer à l'OIM. Ils vont être 111 en 2017.
Poursuivons l’analyse.
En deuxième lieu nous remarquons qu’il existe pas mal de pays sans aucune participation ou alors si peu (max. 3). Il s’agit du Bahrein, du Bénin, du Burkina Fasso, du Sultanat de Brunei, de la Communauté des Etats Indépendants (exception liée à la chute de l’URSS), de Chypre, de l’Egypte, de la Gambie, du Ghana, de l’Irak, de la Jamaïque, du Kenya, du Laos, de Madagascar, de Myanmar, du Mozambique, de la Mauritanie, du Nicaragua, du Népal, de la Serbie-et-Montenegro, des Emirats Arabes Unis et du Zimbabwe.
On peut aisément les classer en deux catégories : les pays riches (en pétrole) et les pays pauvres. Venant de ces pays pauvres on conçoit que ceux-ci veuillent privilégier les J.O plutôt que des Olympiades lesquels n’ont quasiment aucun retentissement médiatique. Mais dans la lutte internationale pour la survie est-ce une bonne stratégie ? Il faut noter que seules les Antilles Néerlandaises n'ont pas participé aux J.O de 2016. Même Haïti y a envoyé une délégation !
Est-ce à dire que le R.O.I entre la formation d'un athlète et celle d'un matheux est en faveur de l'athlète ? S'il s'agit de jeter de la poudre aux yeux de sa population, alors oui. S'il s'agit de survivre à la guerre technologique alors c'est totalement risible.
Revenons à la théorie de l'enseignement des maths dans l'étude de la guerre technologique. L'exemple de Myanmar devrait à ce titre être symptomatique.
Puisque 88 % des Birmans sont bouddhistes ils ne devraient même pas participer à ce concours. Voyons maintenant les chiffres. Pas besoin de copier un tableau, il n'y a que deux chiffres : 99ième en 2017 et 96ième en 2016.
Que dit Wikipédia à leur sujet :
Éducation
La plupart des universités fermées et/ou déplacées en banlieue en décembre 1996 pour des raisons de sécurité ont rouvert leurs portes. Mais la qualité de l'enseignement reste médiocre, notamment du fait de la corruption endémique. Selon l'UNICEF, seulement 28 % des enfants du primaire terminent leur scolarité...
Économie
Le pays est très peu industrialisé, la population est essentiellement rurale (70,4 % selon le recensement en 2014)...
Les événements récents nous montrent à quel point le Myanmar est tombé sous la tutelle du grand frère chinois.
Conclusion : pas de matheux => pas de technologie locale. Pas de technologie et pas de pétrole (pour faire simple) => domination par un puissant voisin.
Quod erat demonstrandum ! Ou CQFD en français.
Un pouce levé quand même pour avoir tenté de concourir à partir de 2016 !
Tournons-nous vers le Bouthan, seul pays au monde qui ne calcule pas son PIB mais son indice de bien-être ! Hé bien, il ne figure même pas dans la liste des concurrents en maths.
Ce pays qui semble tiré du roman d'Aldous Huxley précité, ne subsiste que par le bon vouloir de l'Inde qui s'est positionné à son égard en « grand frère ». Il suffit de se retourner vers le dernier clash politique entre l'Inde et la Chine pour s'en convaincre.
Le raisonnement précédent s'applique de nouveau. Q.E.D.
Apparté :Loin de moi de vouloir me moquer de ce pays. Au contraire j'éprouve pour ce dernier une admiration mythique.
Par contre quid de Brunei, des EAU et du Bahrein ? Pas de matheux chez eux ? Pas de volonté politique de soutenir les maths ? Pas de matérialisme dans ces pays ? Zenitude et pleinitude ? Certes ce sont des tous petits pays mais d’autres aussi petits participent honorablement tels le Luxembourg, le Liechtenstein ou la Lituanie.
Non, ces pays ont fait le choix de vivre de la rente du pétrole car ils en ont, eux. Ces pays ont donc le choix de leurs armes dans la bataille de survie technologie.
Chypre fait dans ce groupe figure d’exception car il appartient plutôt au groupe des riches mais sans pétrole et pourtant Chypre ne participe pas. Le chypriote n’est pas matheux ? Le chypriote est zen ? Sans explication cela va vite tourner au cliché ! Tout simplement Chypre est une île montagneuse qui a su tirer parti de sa position insulaire pour devenir un paradis fiscal. Point n'est donc besoin de matheux pourvoyeur d'industrie.
Poursuivons l'étude des chiffres. On y remarque aussi l'éclatement de l'URSS. Mais nous allons y revenir longuement par la suite.
Etablissons maintenant un comparatif USA/URSS-Russie/Chine/France/Allemagne.
Pourquoi ces 5 pays. Car plus de pays alourdirait la lecture du graphique. Puis parce que les USA, Russie et Chine sont les 3 premiers de la classe (il est toujours sain de se mesurer aux meilleurs). Et pour finir car l'Allemagne est notre sempiternel challenger et à l'aune de laquelle tout ce qui est production française doit se mesurer. C'est devenu un diktat économico-journalistique.
Graphique 1

Habituellement les courbes indiquent que plus les indicateurs sont élevés, meilleurs sont les résultats. Ici c'est exactement l'inverse puisque avoir un « 1 » correspond à être le meilleur.
On observe clairement qu'entre 1967 et 1992, la France luttait presqu'à armes égales avec l'infernal triplette Chine/URSS-Russie/USA. Nos frères ennemis germains, eux, tirant encore mieux leur épingle du jeu.
Curieusement on observe aussi un décrochage franco-germain aux alentours de 1992 : la France perdant en moyenne 20 points tandis que les allemands n'en perdent que 11. Que s'est-il passé en 1992 ? Les causes probables ont-elles des effets immédiats ?
Tout simplement l'éclatement de L'URSS a amené 15 nouveaux pays. Ouf, nous voici rassuré. Non car il semblerait alors que ces 15 nouveaux pays se soient tous glissés devant nous ! Entraînant avec eux en plus 5 autres différents qui seraient soit d'autres nouveau-venus soit d'anciens qui nous auraient surclassé !
Une réalité extrêmement amère point à l'horizon : la Loi des Nombres.
Pour un pays, augmenter le vivier d'où émergerons les prochains compétiteurs en math est plutôt une bonne chose. Pour ce faire il existe 2 solutions (qui ne sont pas exclusives et peuvent être complémentaires) : augmenter sa population et donc en augmenter celle des « matheux ». Ou alors augmenter la population de « matheux » en ne la sélectionnant plus seulement dans un vivier issu d'une « élite » présupposée – sous la Noblesse c'eût été elle, à l'époque actuelle ce serait l'Upper Class.
Nonobstant le côté financier de l'affaire, cela va augmenter la partie droite de la courbe de Gauss constituée par le nombre de nos enfants excellentes matheux. Soit. Mais en extraire seulement 6 (donc la crème des crèmes) nous fait entrer dans la partie anomalie statistique de cette courbe, à son extrême-droite.
Prenons un exemple.
Supposons un pays de 300 millions d'habitants (pays A). Qui voit sa population diminuer de moitié (donc 150 M ou A/2) puis d'encore de moitié (donc 75 M ou A/4) puis d'encore de moitié (37,5M ou A/8) puis 18,75 M ou A/16… Et qu'en plus on dispose encore de ses différents classements successifs alors on pourrait voir à quel moment les anomalies statistiques apparaissent réellement.
Par hasard on dispose d'une telle chance. Il s'agit de l'URSS qui en Juillet 1991 -donc juste avant sa décomposition sociale- a une population de 293 millions d'habitants.
|
Population |
Plus proche |
|
| URSS | 293 | ≈ A |
| Russie | 145 | ≈ A/2 |
| ≈ A/4 | ||
| Ukraine | 47 | ≈ A/8 |
| Ouzbékistan | 27 | ≈ A/16 |
| Biélorussie | 9,5 | ≈ A/32 |
| Lituanie | 3 | ≈ A/64 |
| Estonie | 1,3 | ≈ A/128 |
Graphique 2

Nota : afin de pouvoir comparer la Russie à l'ex URSS j'ai translatée la période soviétique de 1967-1991 à 1992-2017.
On observe qu'entre l'ex URSS et la Russie il n'y a presque pas de différence. Puis qu'à chaque division par 2 supplémentaire le pays concerné perd de plus en plus en terme de rang (remarque 1). Aux 2 notables exceptions prés que constituent la Biélorussie et l'Ouzbékistan dont il faudrait inverser les positions !
On pourrait tirer la conclusion qui consiste à dire que c'était la Russie au sein de l'ex-URSS qui tirait celle-ci par le haut. Certes mais comment expliquer alors la remarque 1 ? Par le fait que les dirigeants de l'URSS auraient curieusement avantagé l'enseignement des maths dans ses satellites en leur donnant des avantages proportionnel à la taille de leur population ?
Je pense que non et qu'il existe une loi de type exponentiel qui lie un pays à la taille de sa population et au rang théorique qu'elle peut espérer atteindre. Et la population minimale de ce pays serait de 150 millions. Ceci est la première Loi (pour paraphraser Isaac Asimov).
Je sais. C'est cruel pour nous. Mais m'objecteriez-vous : « et l'Inde, alors ? Avec son 1,3 milliard d'habitants elle devrait être en pôle position ! Et la Chine ? ».
C'est là qu'intervient une des premières pondération à cette loi. Appelons-la « deuxième Loi ». Et l'on revient à la problématique de l'escrime. Quel ratio nombre d'élève de Terminale S/population totale l'Inde ou la Chine ont-ils ? Est-ce le même que celui de la Russie ou des autres pays occidentaux ?
En fait ici on ne doit comparer que le nombre d'élève en Terminale S de chaque pays. Soit pour la France 173000 en 2016.
Et pour l'Inde 1 million environ en 2012-13.
Même avec ce premier filtre l'avantage en nombre reste en faveur de l'Inde. Alors pourquoi l'Inde a-t-elle un rang en moyenne très moyen (si je peux me permettre ce jeux de mots très moyen !) et particulièrement en chute depuis 2004 ?
Graphique 3

Répondre à cette question c'est aussi répondre pourquoi l'Inde loue une partie de ses sous-marins nucléaires à la Russie, pourquoi elle ne produit pas ses avions de combat, pourquoi elle n'a pas d'équivalent TGV , ne construit pas elle-même ses centrales nucléaires...La réponse est à chercher dans la volonté politique de ses dirigeants. Ces derniers ne mettent tout simplement pas l'accent sur l'enseignement des maths. Il s'ensuit que sa R&D qui en découle n'est pas aussi efficace qu'elle devrait l'être eu égard à sa population.
Le troisième enseignement que l'on peut retirer de ces analyses est qu'un pays qui a dépassé ce seuil de 150 M n'a pas automatiquement accès à l'élite mathématique. Il doit la former ! Trivial mais imparable. Il s'agit de la troisième Loi.
En résumé.
Un pays possède une population maximale de fort en math en devenir, directement lié à la taille de sa population globale (Loi 1). Pour détecter tous ces fort en math en devenir, il faut que cette détection se fasse sur l'ensemble de la population et non pas sur une partie réputée potentiellement plus prometteuse du fait de son éducation au sens large (Loi 2). Et pour finir qu'il investisse suffisamment dans ce potentiel humain détecté (Loi 3).
L'Histoire montre clairement que les dirigeants d'un pays peuvent de façon prépondérante influer sur ces 3 points. Nous avons déjà vu le cas de la France et de Napoléon. En voici un autre.
Au 18ième siècle les plus grands scientifiques de l'époque étaient français ou anglais. Prenant ombrage de ce constat Frédéric 2 de Prusse décida d'y remédier et de mettre le paquet (loi 3) sur l'enseignement populaire (loi 2) et sur celui des sciences (loi 3). Les résultats ne seront visibles que 30 ans plus tard quand les premiers noms de la Science allemande firent leur apparition.
Et depuis le leg de cette volonté se perpétue outre-Rhin puisque les allemands nous surclassent depuis le début des OIM ! (cf graphique 1)
Revenons à l'Inde et à son challenger en terme de population, à savoir la Chine.
La Chine, elle, elle y a mis le paquet ! Elle truste la première place régulièrement aux OIM. Et que voit-on ? Elle est en tête actuellement dans la compétition spatiale mondiale -Graal scientifique s'il en est. Et je ne parle même pas de sa production industrielle qui via sa branche « armée » commence à inquièter.
Et du côté de la France ? Car c'est cela qui nous intéresse au premier chef. Comment interpréter nos résultats ?
La première lecture du graphique 1 indique 2 périodes : il y a un avant et un après 1992.
Avant 1992, nous étions en moyenne 10ième, puis nous sommes passés 30ième !
Au titre de comparaison avec les pays issus de l'explosion soviétiques, nous avons à peu prés la population de l'URSS divisé par 4 (ou A/4). Il n'y a pas de A/4 dans les ex-républiques soviétiques. On se tourne donc vers A/8 qui est l'Ukraine. Nous devrions -ceteris paribus- être devant l'Ukraine puisqu'on compare un A/4 avec un A/8 (avec A/8 largement inférieur à 150M).
Pas du tout !
Graphique 4

On note que malgré la révolution de Maïdan en 2014 et les troubles conséquents qui s'en sont ensuivis, ce pays sait garder son rang. Ce qui tend à prouver qu'il existe une forte inertie dans toute la structure administrativo-sociétale relativement à l'enseignement des mathématiques en Ukraine !
Pour comprendre toute l'étendue du désastre -qui en est un vrai- il faut entrer dans les coulisses de l'OIM.
Nous savons déjà que cette compétition a lieu tous les ans. Chaque pays participant envoie 6 de ses meilleurs éléments du secondaires (pour la France ce sera quasi exclusivement des élèves de Terminale).
Les épreuves sont au nombre de 6 (numérotées de P1 à P6). Elles se déroulent sur deux journées à raison de 4h30 par jour (P1 à P3 le 1er jour, P4 à P6 le deuxième).
Les matières au programme sont la Géométrie, l'Algèbre, l'Arithmétique, Combinatoire.
Traditionnellement il y a 2 épreuves en Géométrie, les 4 matières restantes se répartissant entre les 3 épreuves restantes.
Les épreuves P1 et P4 sont élaborés afin qu'elles soient considérées comme faciles -pour la population ciblée bien sûr ! P3 et P6 sont réputées très dures. P2 et P4 sont de difficulté intermédiaire.
Les notes sont établies à partir des copies ET des brouillons rendus. Ainsi même un résultat faux rendu sur copie peut être rétribué de points si le brouillon indique par exemple un bon raisonnement.
Chaque matière est notée de 0 à 7.
Il n'est donc pas étonnant que pour des pays « moyens » les candidats obtiennent ce type de tableau.
◄ Arménie ►
◄ 58ieme OIM 2017
| Compétiteur [♀♂] | P1 | P2 | P3 | P4 | P5 | P6 | Total | Rang | Récompense | |
|---|---|---|---|---|---|---|---|---|---|---|
| Abs. | Rel. | |||||||||
| Résultats d'équipe | 41 | 18 | 0 | 38 | 2 | 0 | 99 | 41 | 63,64% | A, A, B, B, H |
| Mikayel Mkrtchyan | 7 | 6 | 0 | 7 | 0 | 0 | 20 | 103 | 83,39% | Médaille d'argent |
| Gagik Magakyan | 7 | 4 | 0 | 7 | 1 | 0 | 19 | 115 | 81,43% | Médaille d'argent |
| Sergey Nersisyan | 7 | 4 | 0 | 7 | 0 | 0 | 18 | 139 | 77,52% | Médaille de bronze |
| Vahan Martirosyan | 7 | 3 | 0 | 7 | 1 | 0 | 18 | 139 | 77,52% | Médaille de bronze |
| Vahe Karagulyan | 7 | 1 | 0 | 7 | 0 | 0 | 15 | 292 | 52,61% | Mention honorable |
| Natali Muradyan | 6 | 0 | 0 | 3 | 0 | 0 | 9 | 471 | 23,45% | |
Adjoint : Smbat Gogyan
Analyse :
-Les arméniens s'illustrent plutôt excellemment pour un pays de 3 M soit un A/64. Les épreuves P1 et P4 (donc les dites “plus faciles”) sont résolues à la perfection pour 5 d'entr'eux avec un fléchissement pour le 6ième candidat.
-Les épreuves de moyenne difficulté (P2 et P5) constituent une marche qu'aucun ne parvient à franchir complètement. L'exercice P2 établit à lui seul le classement des arméniens entre eux. La matière dont la problématique a été tirée semble avoir été vue au programme. Ici c'est la valeur individuelle qui fait la différence.
-On constate une grande homogénéité d'échec à P5. La matière dont la problématique a été tirée semble ne pas avoir été abordée à l'école.
-Quant aux épreuves P3 et P6 c'est l'impasse totale.
Synthèse de ce tableau
-Les compétiteurs sont de talent au vu de la taille de leur pays.
-L'épreuve P2 les départagent et montre leur disparité liée au critère population.
-Les résultats aux épreuves dures P3 et P6 indiquent clairement un manque de préparation.
-Une matière entière liée à P5 échappe plus ou moins au programme ou du moins n'existe que dans une version édulcorée.
-Et une dernière remarque qui va entrainer bien des polémiques j'en suis sûr : les candidats sont remarquablement “locaux” : tous leurs noms sonnent parfaitement arméniens avec leur finale en “yan”. Je ne veux indiquer par cette remarque ceci et que ceci : à l'inverse du foot, pour ces OIM, l'Arménie n'a pas “acheté” de compétiteurs étrangers à prix d'or. Pour poursuivre la métaphore : les candidats sont issus des CFA de leur Club.
Prenons les USA.
◄ États-Unis d'Amérique ►
◄ 58ieme OIM 2017
| Compétiteur [♀♂] | P1 | P2 | P3 | P4 | P5 | P6 | Total | Rang | Récompense | |
|---|---|---|---|---|---|---|---|---|---|---|
| Abs. | Rel. | |||||||||
| Résultats d'équipe | 42 | 29 | 0 | 42 | 23 | 12 | 148 | 4 | 97,27% | O, O, O, A, A, A |
| James Lin | 7 | 7 | 0 | 7 | 7 | 2 | 30 | 6 | 99,19% | Médaille d'or |
| Andrew Gu | 7 | 4 | 0 | 7 | 7 | 1 | 26 | 30 | 95,28% | Médaille d'or |
| Ankan Bhattacharya | 7 | 5 | 0 | 7 | 7 | 0 | 26 | 30 | 95,28% | Médaille d'or |
| Zachary Chroman | 7 | 2 | 0 | 7 | 1 | 7 | 24 | 49 | 92,18% | Médaille d'argent |
| Junyao Peng | 7 | 7 | 0 | 7 | 0 | 1 | 22 | 72 | 88,44% | Médaille d'argent |
| Vincent Huang | 7 | 4 | 0 | 7 | 1 | 1 | 20 | 103 | 83,39% | Médaille d'argent |
Adjoint : Brian Lawrence
Tirons directement la synthèse.
-Les compétiteurs ne sont si talentueux que ça au vu de la taille de leur pays. Avec un pays à A ils devraient faire le plein (Loi 1) !
-Cette fois-ci c'est P2 et P5 qui sélectionnent en interne. Les matières sont vues par tous mais tous ne les maîtrisent pas.
-Les résultats aux épreuves dures P3 et P6 indiquent clairement un manque de préparation avec une notable exception pour Zachary Chroman qui y obtient un 7. Et P3 met tout le monde d'accord !
-Et la dernière remarque quant aux noms...Quand on sait que les noms aux USA suivent les groupes ethniques, soit dans par ordre décroissant : anglo-saxon puis espagnols...
Quatre noms d'origine asiatique, un indien et le dernier que je laisse au bénéfice du doute aux anglo-saxons. Même l'entraîneur n'échappe pas à ce constat. C'est le Real de Madrid !
Le premier de la classe :la Chine
◄ République populaire de Chine ►
◄ 58ieme OIM 2017
| Compétiteur [♀♂] | P1 | P2 | P3 | P4 | P5 | P6 | Total | Rang | Récompense | |
|---|---|---|---|---|---|---|---|---|---|---|
| Abs. | Rel. | |||||||||
| Résultats d'équipe | 42 | 25 | 0 | 42 | 19 | 31 | 159 | 2 | 99,09% | O, O, O, O, O, A |
| Qiuyu Ren | 7 | 7 | 0 | 7 | 7 | 4 | 32 | 4 | 99,51% | Médaille d'or |
| Lu Zhang | 7 | 7 | 0 | 7 | 2 | 5 | 28 | 14 | 97,88% | Médaille d'or |
| Jinze Wu | 7 | 4 | 0 | 7 | 7 | 1 | 26 | 30 | 95,28% | Médaille d'or |
| Tiancheng He | 7 | 4 | 0 | 7 | 0 | 7 | 25 | 36 | 94,30% | Médaille d'or |
| Yuanyang Jiang | 7 | 2 | 0 | 7 | 2 | 7 | 25 | 36 | 94,30% | Médaille d'or |
| Xingjian Zhou | 7 | 1 | 0 | 7 | 1 | 7 | 23 | 64 | 89,74% | Médaille d'argent |
Adjoint : Sihui Zhang
J'ai retiré les résultats de 2017 car ils ne sont pas du tout représentatif de ce que la Chine produit habituellement. Il s'agit d'un accident qui a sûrement une explication liée au programme de math chinois. Si vous voulez un résultat phénoménal allez jeter un oeil au cru 2013.
-P3 et P6 établissent la sélection en interne.
-Pour le reste, quasi carton plein. Ce qui est normal pour un pays de presque 4A.
Quant aux “joueurs” ils sont tous issus du CFA d'Auxerre avec Guy Roux comme entraîneur.
Et la France dans tout ça...
◄ France ►
◄ 58ieme OIM 2017
| Compétiteur [♀♂] | P1 | P2 | P3 | P4 | P5 | P6 | Total | Rang | Récompense | |
|---|---|---|---|---|---|---|---|---|---|---|
| Abs. | Rel. | |||||||||
| Résultats d'équipe | 41 | 11 | 0 | 32 | 16 | 0 | 100 | 39 | 65,45% | A, A, B, B, H, H |
| Baptiste Serraille | 7 | 0 | 0 | 7 | 7 | 0 | 21 | 82 | 86,81% | Médaille d'argent |
| Yakob Kahane | 7 | 3 | 0 | 2 | 7 | 0 | 19 | 115 | 81,43% | Médaille d'argent |
| Joachim Studnia | 7 | 3 | 0 | 7 | 0 | 0 | 17 | 188 | 69,54% | Médaille de bronze |
| Olivier Garçonnet | 7 | 1 | 0 | 7 | 2 | 0 | 17 | 188 | 69,54% | Médaille de bronze |
| Timothée Rocquet | 6 | 1 | 0 | 7 | 0 | 0 | 14 | 342 | 44,46% | Mention honorable |
| Ilyas Lebleu | 7 | 3 | 0 | 2 | 0 | 0 | 12 | 416 | 32,41% | Mention honorable |
Adjoint : Vincent Jugé
J'ai été dur car en 2017 nous étions 39ième et tandis que l'année d'avant 25ième. Mais c'est voulu. Cela fait ressortir beaucoup plus de choses.
-On est juste derrière l'Arménie...à la 41ième place, alors que nous sommes un pays A/4. On est en train de comparer un pays de 69 M d'habitant à un pays de 3 M, là !
-Même les épreuves P1 et P4, faciles, ne le sont manifestement pas pour la moitié de nos français.
-Il existe une grosse disparité quant à la résolution des épreuves moyennement dures.
-Quant aux épreuves dures : pschitt, circulez...
-Pour ce qui est des joueurs on est dans du Club qui n'a pas les moyens, qui recrute local et qui joue en Division d'Honneur. Ici s'arrête ma comparaison avec des clubs de foot : je ne veux pas me mettre à dos le FC de Trifouilli-les-deux-cimetières !
J'insiste absolument sur ce fait : individuellement les candidats font de leur mieux : personne ne va de gaîté de coeur se faire écharper sur un champ de bataille. Les candidats y vont en sachant que leur préparation scolaire associé aux quelques stages de préparation supplémentaires “spécial OIM “ne leur permet pas de faire mieux.
Et c'est tout à leur honneur ! En 2017 ils étaient 39ième mais 25ième en 2016 ce qui constitue un véritable exploit si on met la barrière haute à la 30ième place ainsi que la fixe l'entraîneur-même de l'équipe française dans un article de 2012 !
“Force est de constater que la France ne peut plus raisonnablement envisager un classement qu’autour de la 30e place. Sans entrer dans un débat sur l’enseignement des mathématiques en France, on peut avancer deux raisons à cela :”
Puis il énumère les 2 raisons que je vais résumer ici :
-L'éclatement de l'URSS a amené 15 nouveaux pays compétiteurs de talents. Ces pays ont une très forte tradition mathématique et la transpose fortement dans la réalité.
-L'implication accrue de certains pays compétiteurs depuis 1992 dans la préparation de ses candidats à l'OIM.
Concernant son premier argument : les pays issus de l'éclatement sont impitoyablement soumis à la Loi 1 (les deux autres lois -mal appliquées- ne peuvent que diminuer le classement). Or aucun de ces nouveaux pays ne nous concurrence en matière de population. Ce qui veut logiquement dire que si un de ces pays nous passe devant cela est de notre entière faute. La meilleure preuve en est le trio USA/Chine/URSS-Russie qui a parfaitement encaissé le nombre supplémentaire de pays compétiteurs et sont restés peu ou prou à leur place.
Il s'agit plutôt de rechercher comment la France décline dans la réalité cette grande tradition mathématique qui a fait notre réputation et pourquoi nous n'en avons plus que les oripeaux.
Sur le deuxième point il a tout à fait raison. Alors que 1992 nous fait perdre -sur les 2 périodes sus-mentionnées- 20 points (10ième à la 30ième place), il n'en fait perdre à l'Allemagne que 11 (qui passe de la 5ième à la 16ième place) et qui en fait même gagner une à l'Italie (29ième à la 28ième) ! Voici deux pays qui ont sûrement dû valoriser les lois 2 et 3.
L'homme étant du sérail, il émet des critiques très feutrées expliquant les résultats médiocres depuis 1992. Il dit ne pas vouloir entrer dans la polémique du programme scolaire. Cela Jean-Paul Brighelli le fait parfaitement dans son livre « La fabrique du crétin ». Je reviendrais sur ce point essentiel dans la conclusion.
Le site de l'OIM, abondamment pourvu de chiffres le confirme également. Si les programmes ainsi que leur enseignement étaient inchangés, les résultats par équipe devraient être sensiblement égaux durant ces 2 périodes. Car ici il ne s'agit plus de se comparer aux autres mais à soi-même en valeur absolue.
Soit justement à comparer un 30ième rang de 2010 à un 10ième rang de 1992.
Effectivement nous étions en moyenne 10ième avant 1992 et 30ième après. Si un 30ième rang de 2010 valait (en nombre de points et non plus en terme de rang) un 10ième rang, on devrait obtenir un nombre de points un peu inférieur (un peu car il faut tenir compte du fait que les épreuves deviennent de plus en plus dures).

Il m'est tellement insupportable de devoir comparer des individualités qui sont mes compatriotes, qui sont des jeunes enthousiastes, qui ont mouillé leur maillot sous les couleurs de la France, que je regrette déjà d'avoir mis ce tableau dans cet article. Je le laisse pourtant car flouter les noms ne servirait à rien car tout se trouve sur le site de l'OIM.
Je me contenterais de regarder l'homogénéité des colonnes.
-Il est clair que P5 pose autant de problème en 2010 qu'en 1992. Programme ?
-Il est net qu'en 1992 on savait résoudre du « dur » mais deux candidats avaient aussi du talent (obtenir respectivement 11 et 12 points sur P3 et P6 ce n'est pas rien). Mais ils ont pu le faire car ils avaient été préparés. Seuls les deux premiers de 2010 ont réussi à faire parler leur talent et réussi à « pondre » quelque chose et sont allé grappiller 3 points chacun. Etaient-ils aussi bien préparés que leurs aînés ? Avaient-ils moins de talent qu'eux ? Non et non !
-Pour ce qui est du « facile » il est anormal qu'en 2010 il y ait une tel écart entre P1 et P4. Cela sent le « pas vu » ou le survol rapide du programme.
-Et pour clôturer sans ambiguïté : en 1992 les français ont obtenu un total de 139, la presque génération d'après en 2010 n'en a obtenu que 105. Soit 25 % de moins.
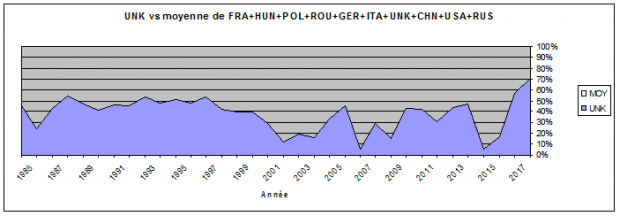
L'OIM permet en très peu de clic d'avoir une foultitude de tableau. Par contre il y manque celui qui permet à un pays de voir sa propre évolution en valeur absolue (le total de ses points et non plus son rang par rapport aux autres pays). D'autre part le nombre de pays participants augmente sans arrêt et donc en toute logique, la difficulté des épreuves (il faut bien séparer les candidats !). Ce qui m'a a mené à produire une comparaison entre la France et un panel composé de France, Hongrie, Pologne, Roumanie, Allemagne, Italie, Royaume-Unis, Chine, USA et Russie, cette comparaison ne se faisant que sur les matières dites « dures » P3 et P6. Car c'est par ces matières que sont mieux mises en exergue les lacunes (liées au critère de population, à la politique d'enseignement...).
En dépit de ce que la Loi 1 m'imposerait envers qui nous comparer, j'ai choisi un panel de pays qui m'a paru parfaitement représentatif d'un challenge mondial : la France par rapport à 3 pays de l'ex-bloc soviétique, à 3 pays de l'ex-Europe de l'Ouest et comparable en taille, et au trio de tête.
Le type de diagramme choisi permet aussi de s'affranchir du phénomène lié à l'augmentation de la difficulté des épreuves, la somme de l'indicateur MOY et de celui de FRA étant toujours égale à 100 %. Quand l'indicateur FRA dépasse 50 % cela veut dire que la note de la France est supérieure à celle de la moyenne.
D'autre part jusqu'en 1981 le nombre de candidat max était de 8 ; il est passé à 4 en 1982 pour revenir à 6 en 1983. La longueur des extraction étant telle, j'ai préféré débuter la courbe en 1983.
Graphique 5

Il appert clairement que :
1) Nous étions depuis 1983 et jusqu'en 1999 un soupçon en dessous de la moyenne avec une notable exception en 1990 où la France a été en-dessus. Donc nous avions su encaisser le choc de 1992. Ce résultat d'ensemble était normal, voire meilleur, eu égard à la taille de notre pays.
2) Depuis cela chute de plus en plus avec 3 « zéros pointés » en 2013, 2014 et 2017.
Dans un grand élan expiatoire je vais produire le graphique du Royaume-Unis. Voyez la réaction depuis 2014. Sans commentaire...
Graphique 6
Conclusion
Jean-Paul Brighelli a raison (cf lois 2 et 3).
Et pour le résumer : depuis 30 ans (son livre date de 2005 donc le début se situe en 1985) les livres -et incidemment les programmes- ont subi une cure de maigreur et ont été réduits de 2/3 environ. Cela se ressent aux résultats depuis 2000. Ce phénomène se double par la mise en place depuis 2010 de la nouvelle génération de professeurs ayant « bénéficié » de cette cure.
Pensez-vous que l'enseignement de ces derniers par un phénomène osmotique transgénérationnel égale celui de leurs prédécesseurs ? Les lois 2 et 3 sont venues frapper avec force tandis que la loi 1 nous érode. Le différentiel de croissance de population de la France par rapport au reste du monde n'est pas en notre faveur (loi 1 en notre défaveur). Et nous tentons de l'endiguer pour nous permettre de rester dans la course en favorisant une maigre élite mathématique extraite du tamis des écoles d'excellence -les big four parisiennes et l'école du Parc à Lyon pour la province (mauvaise utilisation des lois 2 et 3), écoles alimentées par les enfants de Monsieur ToutLeMonde comme chacun sait !
Pensez-vous que la nouvelle génération d'ingénieur français va nous emmener sur Mars ?
Je vais clore cette étude par une micro analyse (qui mériterait un article tout entier) d'un comparatif France/Iran/Israël.
Graphique 7

La première femme a obtenir la médaille Louis Field en 2014 est iranienne (malheureusement décédée en 2017 à l'âge de 40 ans). Maryam Mirzakhani a obtenu 2 fois la médaille d'or aux OIM en 1994 et 1995.
Est-ce un hasard ?
Est-ce un hasard si en 2004, l’Iran comptait plus de 2,2 millions d’étudiants à l’université dont 60 % de filles pour une population de 83 millions d'habitants ? Soit le même chiffre que les allemands qui ont presque la même population.
L'Iran a fait une magnifique utilisation des 3 lois !
J'ai cité Israël car géographiquement ces 2 pays sont tout proches. Et si quasi tout les distingue, une chose les unit cependant : l'amour des sciences. Par contre on voit nettement qui va prendre l'ascendant sur les deux autres. Et ce grâce à quoi ?
Grâce à une politique intelligente d'enseignement des mathématiques !
39 réactions à cet article
Ajouter une réaction
Pour réagir, identifiez-vous avec votre login / mot de passe, en haut à droite de cette page
Si vous n'avez pas de login / mot de passe, vous devez vous inscrire ici.
FAIRE UN DON










