H (Ψ) = E Ψ : La matière n’existe pas ; tout n’est que forme et énergie
Cette fois je me décide à vous faire partager l’une des découvertes les plus surprenantes de ces dernières années. Le texte qui suit a été publié en annexe à ma thèse (Procès et Miroir, éléments de métaphysique, Poitiers, 1996) puis remanié pour être intégré comme un chapitre dans un essai sur la fin du matérialisme. Seules quelques personnes ont pu avoir accès à ce texte. L’édition étant parsemée d’obstacles, je me décide à publier cette découverte pour la partager. Par ailleurs, étant donné que ce texte a circulé chez quelques personnes du monde de l’édition, je préfère que cette découverte soit présentée ici par mes soins plutôt que remanié par un improbable épistémologue qui pourrait s’en attribuer la paternité. Pour la petite histoire, cette étude a été effectuée suite à une requête du rapporteur de thèse Hervé Barreau afin d’appuyer une analyse de la métaphysique d’Aristote dans laquelle j’avais lancé avec une désinvolte intuition la thèse de la dualité forme énergie dans la théorie quantique, en relation avec mon interprétation de l’hylémorphisme aristotélicien sous l’angle d’une dualité forme et… non pas matière, mais mouvement. Et donc, je me suis farci du Schrödinger et un peu de mathématique quantique pour arriver à ce résultat épistémologique fondamental. La matière répond en fait à une dualité forme et énergie, lesquelles peuvent être déduites d’une analyse quantique. Cette découverte appuie le nouveau paradigme en s’inscrivant dans le cadre des nouvelles orientations « ontologiques » sur l’importance de l’entropie et de l’information qui est, selon Vlatko Vedral, un donné fondamental de l’univers. Bonne lecture. N’attendez pas une quelconque application pratique mais sachez apprécier le plaisir de connaître l’univers dans lequel vous existez. Ce n’est que le début d’une révolution ontologique.
LA DUALITÉ FORME ÉNERGIE DANS LE MONDE QUANTIQUE
1 L’équation de Schrödinger et la séparation forme/énergie
Dans la théorie quantique de l’atome, le formalisme mathématique utilise la superposition de fonctions d’onde complexes dont on vient de dire quelques mots. Cette représentation a été initiée par les travaux de de Broglie et Schrödinger, fondateurs en 1924-1925 de la mécanique ondulatoire qui en réalité, est mathématiquement équivalente à la mécanique quantique développée indépendamment par Bohr et ses collaborateurs. Dans le formalisme ondulatoire, la fonction d’onde est une fonction complexe, aussi, on ne peut tirer directement de cette fonction un paramètre physique observable. Cette fonction obéit à une équation d’onde décrivant son évolution au cours du temps. La solution de cette équation doit permettre d’établir la forme que prend le “mouvement” de la particule, ou bien la trajectoire si l’on raisonne classiquement.
L’équation d’onde est appelée équation de Schrödinger. Celui-ci l’a en effet établie par un raisonnement déductif basé entre autres choses sur le principe de conservation de l’énergie. Les symboles utilisés sont les suivants :
dérivation partielle : ∂ / ∂ t , ∂2 /∂x2
fonction d’onde : Ψ (x, y, z, t)
laplacien : Δ = ∂2 /∂x2 + ∂2 /∂y2 + ∂2 / ∂z2
constante de Planck : h, h = h/2π
vecteur position : r = (x, y, z)
masse de la particule : m
potentiel : V(r)
La fonction d’onde associée à une particule est une fonction complexe définie pour tout point de l’espace et du temps. L’équation de Schrödinger détermine son évolution spatio-temporelle Cette équation devrait alors permettre le calcul de la fonction d’onde associée à une particule dotée d’un mouvement non relativiste en présence d’un potentiel défini en tout point de l’espace. Cette équation s’écrit de la manière suivante :
ih ∂ Ψ / ∂ t = - h2/2m Δ Ψ + V.Ψ
L’équation devient utile si elle permet de trouver une fonction d’onde solution pour une particule donnée, et en particulier, pour une particule évoluant en présence d’un potentiel comme par exemple un électron distribué autour d’un proton (atome d’hydrogène). On sait que l’intégration directe de l’équation n’est possible que dans certains cas, et notamment, lorsque l’on cherche des solutions stationnaires. Dans ce cas, on pose une contrainte sur la fonction d’onde et on cherche des solutions à variables séparées où la fonction d’onde est constituée par le produit d’une fonction dépendant uniquement du temps et d’une fonction dépendant uniquement de l’espace.
Soit : Ψ (r, t) = Ψ1 (r ) Ψ2 (t) une telle fonction
En reportant cette fonction dans l’équation initiale, on obtient la formule suivante :
- h2/2m Ψ2 Δ Ψ1 + V.Ψ1 . Ψ2 = ih Ψ1 ∂ Ψ2/ ∂ t
divisons alors par le produit : Ψ1 . Ψ2
ce qui donne la formule suivante comprenant un membre de gauche et un membre de droite :
- h2/2m Δ Ψ1 / Ψ1 + V (r) = ih (∂Ψ2 / ∂ t) / Ψ2
L’égalité entre une fonction spatiale et une fonction du temps n’est possible que si chaque membre est égal à une constante que l’on va poser égale à E (qui sera en fait l’énergie comme on va le constater).
On obtient ainsi deux équations séparées, l’une que doit vérifier la fonction du temps, et l’autre la fonction d’espace. Ainsi le membre de gauche correspond à l’équation pour la fonction spatiale qui ne dépend pas du temps ; notons que cette manipulation mathématique impose une contrainte sur le potentiel V qui ne doit pas dépendre du temps, ce qui notamment est le cas pour le potentiel électrique de l’électron disposé autour du noyau. Puis pour le membre de droite nous obtenons une équation qui détermine une fonction définie uniquement pour le temps. Le sort de l’équation de la fonction temporelle est vite réglé étant donné que l’intégration est triviale, ce qui donne en introduisant une constante C :
Ψ2 = C e iEt/h
La solution partiellement définie et complète de l’équation est donc composée du produit d’une fonction spatiale (indéfinie car il faut intégrer l’équation pour l’obtenir) et d’une fonction du temps qui elle, vient d’être intégrée, d’où la fonction d’onde complète associée à la particule quantique.
Ψ (r, t) = C. Ψ1(r) . e iEt/h
On sait par ailleurs que les observables physiques sont données par des opérateurs agissant sur les fonctions d’onde (ce sont les valeurs propres réelles en raison de l’hermiticité des opérateurs), et pour l’énergie, l’opérateur est défini ainsi :
ih ∂ / ∂ t
Si on fait agir cet opérateur sur la fonction d’onde complète on obtient alors une valeur propre qui n’est autre que E, la constante introduite précédemment. On vérifie ainsi que cette constante introduite arbitrairement (en apparence) n’est autre que l’énergie. La fonction d’onde complète est donc constituée par une fonction spatiale multipliée par une fonction temporelle. Cette fonction temporelle est une fonction périodique dont la période est donnée par la valeur E de l’énergie qui est l’énergie déterminée de l’état stationnaire dans lequel se trouve la particule.
Admettons que l’on veuille formaliser le mouvement d’une particule en présence d’un potentiel, sous condition que ce mouvement corresponde à un état stationnaire (l’énergie de cet état est invariante, tandis que la fonction d’onde est le produit d’une fonction spatiale par la fonction temporelle associée à l’énergie). Pour cela, il suffit d’intégrer dans la mesure du possible l’équation déterminant la solution d’onde spatiale. Il reste à interpréter la signification de la fonction d’onde qui d’un point de vue physique, ne correspond à rien de réel. Le postulat quantique énoncé par Born a permis de raccorder l’image abstraite du formalisme à une image plus physique où notamment les paramètres mesurables sont impliqués. Dans le cas particulier de la fonction d’onde spatiale, on peut calculer la probabilité de présence de la particule dans un domaine donné de l’espace. Pour cela, il suffit de sommer dans ce domaine de l’espace le carré de la fonction d’onde. Or, si cette sommation s’effectue sur la fonction complète, on s’aperçoit que la fonction temporelle ne joue aucun rôle étant donné que son carré est toujours égal à un, et donc, on peut laisser de côté la fonction temporelle dépendant de l’énergie.
On obtient ainsi une densité de présence de la particule dans l’espace pour un état stationnaire donné, correspondant à une solution de l’équation spatiale. La fonction temporelle est mise de côté, elle n’existe plus ! Du moins, elle n’existe plus pour ce qui caractérise un état stationnaire car seule importe la fonction d’onde spatiale permettant de calculer la densité de présence pour chaque domaine de l’espace. La fonction d’onde spatiale indique alors la forme que prend la densité de présence de la particule. Cette forme peut alors être visualisée en représentant la densité avec des zones plus ou moins foncées selon sa valeur relative.
Cependant, l’énergie n’a pas disparu étant donné qu’elle reste la constante qui associe les deux membres de l’équation obtenus par séparation entre fonction spatiale et fonction temporelle, et que de plus, cette constante figure en tant que paramètre dans l’équation spatiale. En d’autres termes, on ne sait pas pourquoi, mais on sait mathématiquement que l’énergie figure dans l’équation spatiale, ce qui signifie que l’énergie est liée (dans le formalisme) à l’équation spatiale, et donc participe à la détermination de la forme d’un état stationnaire, car un tel état est déterminé par la solution de l’équation (où figure E) et que cette solution détermine la forme que prend la densité de présence dans l’espace de cette particule.
On peut donc conclure à une représentation quantique duale faite d’une composante formelle et d’une composante énergétique. Comme par ailleurs la théorie quantique adhère aux résultats de mesure, on peut parler d’une représentation conforme à une nature intelligée en séparant la forme et l’énergie.
L’équation d’onde spatiale peut être appliquée en particulier à l’étude de l’atome d’hydrogène. Grâce aux résultats obtenus, on pourra confirmer le schéma dual construit autour de la forme et de l’énergie. On en verra une illustration éclatante.
2 Théorie quantique de l’atome d’hydrogène
L’atome d’hydrogène est composé d’un électron et d’un proton. Aussi, il faut prendre en compte deux particules. Mais au prix d’une transformation mathématique triviale, on peut obtenir deux équations dont l’une décrira le mouvement relatif de l’électron par rapport au proton. C’est cette équation qui nous intéresse car elle détermine la forme que prend le nuage électronique autour du proton. Dans ce cas, la fonction potentielle (potentiel d’attraction coulombien) prend une forme à symétrie sphérique étant donné qu’elle ne dépend que de la distance séparant l’électron du proton :
V = -K/r où K est une constante connue
Dans ces conditions, l’équation de Schrödinger (spatiale, c’est à dire concernant les solutions stationnaires) s’intègre au prix d’un travail fastidieux en changeant le système des coordonnées cartésiennes et en adoptant un système de coordonnées sphériques comprenant le paramètre radial r qui représente la distance de l’électron au noyau, et deux paramètres angulaires spécifiant l’orientation de l’électron. La forme de l’équation de Schrödinger est modifiée. Puis, on cherche une solution qui soit le produit d’une fonction radiale (dépendant de r) et d’une fonction angulaire (dépendant des deux angles), d’où une séparation entre deux équations qui s’intègrent séparément.
Les solutions ont multiples, et dépendent de trois nombres quantiques qui jouent des rôles bien spécifiques et qui sont : n, l, m (Rivail, 1989, chap. 1 et 2). Le nombre n est important, car chaque n correspond à un niveau énergétique. La valeur de l est alors comprise entre o et n-1, tandis que m est compris entre l et -l. Par exemple, si n = 3, alors l peut prendre comme valeur 0, 1, 2, et m peut prendre comme valeur -2, -1, 0, 1, 2. La solution est donc constituée par le produit d’une fonction radiale dépendant de n et l, et d’une fonction angulaire dépendant de l et de m. On s’aperçoit donc de la “richesse formelle” du formalisme que l’on peut indiquer en exemplifiant une fonction radiale R (r) et une fonction angulaire Y (θ, χ) :
R 2, 1 = (Z/a)3/2 1/2√6 . Zr/a . e -Zr/2a
Y 3, +1 = √31/8√π . sin θ (5 (cos θ)2 - 1 ) e iχ
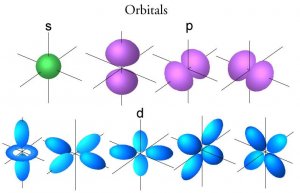
Il faut revenir à la signification physique (réelle-objectiviste) du formalisme. Pour un état stationnaire, il existe une fonction spatiale de l’électron, laquelle indique une densité de présence (proportionnelle au carré de la F.O. spatiale) de cet électron qui ne peut plus être représenté comme un point matériel évoluant dans un espace pourvu de trois coordonnées. On peut tracer des schémas en noircissant des zones plus ou moins foncées en fonction de la densité de présence (Feymann, MQ, p. 412). D’après une interprétation objectiviste, cette représentation indique sans doute possible la forme que prend le nuage électronique lorsque l’atome est dans un état stationnaire.
Chaque état stationnaire est dans un niveau énergétique donné qui ne dépend que du nombre n, ainsi, une énergie donnée est associée à plusieurs formes possibles du nuage électronique. Les énergies sont donc quantifiées et peuvent prendre une suite de valeurs discrètes données par la formule :
En = Eo/n2 avec Eo = -13.6 eV
A chaque forme du nuage correspond une valeur de l’énergie car n conditionne la fonction radiale (cependant, il n’y a pas de bijection car le nombre quantique l intervient également dans la forme que prend la fonction radiale). Ainsi, un atome est dans un état stationnaire avec une forme donnée, et une énergie quantifiée, d’où la spécification d’un niveau d’énergie. Cet atome peut alors effectuer une transition avec un changement du niveau d’énergie. On s’aperçoit que si l’atome passe d’un niveau à un autre, l’énergie est modifiée, et donc, il y a absorption ou bien émission d’une quantité d’énergie. Cet échange d’énergie s’effectue alors par le champ électromagnétique. La nature de l’énergie échangée est radiative, avec comme support le photon, et donc c’est un photon d’une certaine fréquence qui est émis ou absorbé, avec la fréquence donnée par la Formule E = hυ, où E correspond exactement à la différence d’énergie entre niveaux, et donc, si l’électron passe n’un niveau n = a à un niveau n = b, alors, l’atome émet ou absorbe un quantum électromagnétique dont la fréquence dépend de la différence d’énergie E(a,b) = E(a)-E(b), c’est-à-dire :
υ = (Eo/a2 - Eo/b2)/h
La mesure de la fréquence des raies d’émission de l’atome d’hydrogène confirme les valeurs calculées par la théorie quantique, ce qui montre la puissance du formalisme de Schrödinger. Compte tenu des autres confirmations expérimentales (notamment la chimie quantique qui découle de la théorie quantique), on constate que ce formalisme abstrait correspond bel et bien à une configuration réelle d’une entité physique, l’atome. Mais ce qui est surprenant, ce n’est peut-être pas la puissance du formalisme, mais la superconsistance de la nature que l’on peut supposer sur la base de l’ensemble des données empiriques et théoriques.
3 Diversification des formes de l’atome et relation avec l’énergie
Lors d’une transition d’un état énergétique à un autre, l’atome change nécessairement de forme, selon un processus qui échappe pour l’instant à toute investigation physique car comme ont pu le souligner les fondateurs du formalisme ondulatoire, la théorie quantique ne dit rien sur les transitions entre états stationnaires. En fait, elle ne dit pas rien, car si elle reste muette sur ce qui se passe à “l’intérieur” de l’atome lors de la transition, elle décrit ce qui se passe à “l’extérieur”, et indique avec précision les valeurs des énergies échangées. Lors d’une transition, un atome est dans un état stationnaire spécifié par une forme (fonction spatiale) et par une énergie, et lors d’une transition, la forme initiale est “dissoute” tandis qu’une forme nouvelle apparaît et qu’un quantum d’énergie est échangé. On constate donc une conjugaison forme/énergie qui intervient lors des transitions atomiques, et qui apparaît de manière plus nette dans le formalisme. Comment alors cette codépendance forme/énergie s’exprime-t-elle ?
La fonction spatiale radiale est corrélée à l’énergie au travers du nombre quantique n qui fixe à la fois la nature de la fonction radiale (car n est un paramètre d’intégration) et le niveau d’énergie par la relation simple qui a été mentionnée précédemment. La fonction radiale pourrait être une fonction de l’énergie si l’on remplace le paramètre n par sa déduction en fonction de l’énergie soit :
n = √ Eo/En
Mais cela se complique dès que n est supérieur à 1 (avec l’introduction des nombres n et l comme paramètres d’intégration). Aussi, la fonction radiale n’est pas en bijection avec l’énergie mais se situe en relation compliquée avec l’énergie. Cette interdépendance peut être illustrée en établissant un tableau mettant en correspondance les énergies et les fonctions radiales. Ce tableau prend la forme suivante pour n = 1, 2, 3 (avec l = 0, 1, 2).
E1 E2 E3
R1,0 *
R2,0 *
R2,1 *
R3,0 *
R3,1 *
R3,2 *
Ce tableau possède une structure matricielle. Cette représentation des relations entre fonctions radiales et niveaux énergétiques confirme la dualité forme énergie qui correspond à une réalité physique partiellement accessible. Chaque état de l’atome mobilise une certaine quantité d’énergie pour réaliser le déploiement objectif d’une certaine forme. Par ailleurs, plusieurs formes utilisent une même quantité d’énergie (d’où la définition d’états dégénérés, ou de spectre énergétique dégénéré). De plus, le tableau proposé ci-dessus n’indique pas la totalité des fonctions car il n’inclut pas les fonctions angulaires qui expriment toute la richesse des formes des nuages électroniques. Les fonctions angulaires ne dépendent pas de n mais sont cependant reliées aux fonctions radiales par le nombre quantique l qui apparaît dans les deux fonctions. Ainsi, pour une énergie de niveau n, on a le choix entre (n-1) fonctions radiales (chacune donnée par l) auxquelles on doit associer l’une des (2l-1) fonctions angulaires (données par l et m). Ainsi, la théorie est surdéterminé formellement, tandis qu’en réalité c’est une seule forme qui est déployée à un moment donné. Si on admet que les déterminations formelles non exprimées subsistent dans la substance subatomique, alors cette substance est formellement surdéterminée.
Revenons à la fonction d’onde complète associée à un électron dans un état donné. Celle-ci est écrite comme le produit de la fonction spatiale et de la fonction temporelle dépendant de l’énergie. Rappelons la forme de cette fonction temporelle : e iEt/h
On peut alors s’interroger sur la signification physique de cette fonction périodique qui pourrait indiquer alors la nature vibratoire du mouvement (voire des processus) permettant de déployer l’électron autour du noyau. On ne peut que conjecturer car si on raccorde le formalisme quantique au réel physique, cette fonction périodique est élevée au carré et disparaît (heureusement) car une fonction complexe utilise un nombre imaginaire, et n’a pas de correspondance avec un paramètre physique (qui doit être réel).
Le formalisme quantique permet de déduire la quantité d’énergie échangée lors d’une transition entre une forme et une autre forme. Cette énergie étant alors fournie ou restituée sous une forme radiative, liée au champ électromagnétique. Il permet aussi, moyennant certaines approximations, de déduire la structure d’autres atomes et des liaisons interatomiques qui en résultent, tout en produisant la richesse formelle du monde moléculaire que les chimistes étudient (Rivail, 1989).
4 Discussion métaphysique
La théorie quantique appliquée à l’atome d’hydrogène dévoile plusieurs aspects de la réalité, et notamment, la nature hyperformelle du réel que l’on dit matériel. La forme est associée à l’énergie. Plus exactement, la réalité est faite d’un substrat formellement surdéterminé, tandis qu’une certaine quantité d’énergie est associé aux expressions des formes, ainsi qu’aux transitions d’une forme à une autre. Seule, une forme est exprimée, tandis que les autres subsistent dans un domaine non exprimé, sorte de champ fondamental. La possibilité d’extraire mathématiquement l’énergie n’est pas uniquement une propriété de la théorie atomique. C’est un trait presque universel du monde quantique car dans la plupart des cas, on peut calculer l’énergie d’un état à partir d’un outil mathématique, l’opérateur hamiltonien.
La deuxième conclusion fondamentale dérive de la précédente, et concerne la priorité ontologique de la forme sur l’énergie. C’est en effet la forme, surdéterminée par ailleurs dans le champ fondamental, qui détermine l’énergie. Cette priorité de la forme se manifeste notamment lors des transitions entre forme (états) atomiques qui mobilisent une certaine quantité d’énergie dépendant des deux formes, l’antécédente et la suivante. Cette énergie est alors émise ou absorbée selon les nécessités des deux formes associées chacune à un niveau d’énergie. On doit donc admettre que la forme “pilote” l’énergie. Il s’agit donc d’un renversement important car l’énergie est mise au second plan par rapport à la forme, et même à la structure si on admet que le champ quantique fondamental se dévoile comme une énergie particulière car non exprimée et hyperstructurée.
Il reste à expliquer pourquoi ce serait la forme qui déterminerait l’énergie. La conjecture formaliste peut faire appel à un certain nombre d’arguments parmi lesquels la dégénérescence du spectre énergétique montre que c’est la forme (fonction d’onde spatiale) qui est prééminente, et que cette forme est en correspondance avec une certaine énergie “choisie” dans un spectre plus réduit que celui des formes. La signification physique permet de dire que cette énergie concourt (dans l’atome) à réaliser une certaine forme déployée. Si on développe une argumentation résolument réaliste, alors on admet que les autres formes restent à l’état non déployé, c’est-à-dire à l’état de forme substantielle
Si l’on inclut de plus un argument dynamique (voire ontophysique), alors, il faut examiner ce qui se passe lors d’une transition entre états. Une chose est sûre, il se produit un échange radiatif, tandis que la transition s’effectue de manière probabiliste (par opposition à prévisible ou bien prédictible). Si on tente d’imaginer une réalité intra-atomique (intrasubstantielle), alors on peut penser qu’au moment de la transition, la forme précédente est dissoute, puis, cette forme est remplacée par une autre (choisie parmi un ensemble de transitions possibles en fonction du champ radiatif en présence). L’argument probabiliste ne permet pas d’assigner une causalité classique pour cette transition, cependant, on admettra qu’il y a une détermination interne en tant que cause efficiente du processus (la nature probabiliste du processus n’est pas contradictoire avec le fait de supposer une cause intra-atomique efficiente).
Quelle prééminence ontologique admet-on alors pour comprendre une transition, s’agit-il d’une détermination formelle qui mobilise une certaine énergie, ou bien d’une énergie qui va déployer une certaine forme ? La dégénérescence du spectre permet d’imaginer une détermination par la forme. En effet, une forme est déterminée par trois nombres quantiques, n, l, m, tandis que l’énergie n’est déterminée que par n. Le primat de la forme sur l’énergie constitue donc une causalité ontologique ; elle ne s’oppose pas à la détermination probabiliste de la transition ; il suffit en effet d’imaginer un réservoir de “formes” en puissance, et un processus aléatoire qui va permettre de lier l’énergie à la forme (respectant la règle du nombre n qui associe fonction radiale et énergie). C’est donc la forme qui détermine l’énergie. Cette conjecture ontologique conduit à admettre une cause interne efficiente formelle pour déployer l’objet atomique appartenant au monde naturel étendu, ce qui constitue une double rupture (i) avec la physique cartésienne-galiléenne, et (ii) avec l’ontologie cartésienne d’une substance étendue matérielle opposée à une substance pensante.
On connaît le rôle qu’a pu jouer la conception hylémorphique aristotélicienne au Moyen Âge. Cette conception conditionne certaines interrogations ontologiques d’importance menées par les théologiens médiévaux, et notamment par Saint-Thomas lorsqu’il se pose par exemple la question de l’union (supposée parfaite) de la matière aux formes dans les entités angéliques non étendues, ou bien alors la question du rôle de la matière vis-à-vis de l’individuation des créatures dotées d’un corps (ce qui suppose une certaine idée de la matière). Sans doute Heidegger avait-il laissé échapper ces problèmes médiévaux, lorsqu’il considéra que la physique quantique ne pouvait fournir de base solide pour construire une ontologie, à moins qu’il n’ait pas perçu les éléments fondamentaux du formalisme tout en concluant à l’impossibilité de construire une essence à partir de ce formalisme (Chevalley, 1990), auquel cas, Heidegger aurait été prisonnier d’une tradition occidentale d’où l’issue déconstructive que l’on connaît, ce qui ne constitue pas la meilleure porte de sortie, bien qu’il faille en passer par là. Pour notre part, on notera la richesse du formalisme quantique que l’on a pu constater en examinant la théorie quantique de l’atome d’hydrogène, et pourtant, il ne s’agit que d’un aspect d’une théorie qui formalise par ailleurs trois types d’interaction ; aussi, on imagine des possibilités (non évidentes pour l’instant) pour construire une ontologie. Il pourrait être possible de passer du point de vue formaliste au point de vue réaliste, puis d’opter pour un réalisme transcendantal (dualiste).
C. CHEVALLEY, “La physique de Heidegger”, Les études philosophiques, 289-311 (1989).
J.-L. RIVAIL, “Chimie quantique”, InterEditions, Paris (1989).
151 réactions à cet article
Ajouter une réaction
Pour réagir, identifiez-vous avec votre login / mot de passe, en haut à droite de cette page
Si vous n'avez pas de login / mot de passe, vous devez vous inscrire ici.
FAIRE UN DON












